Comprendre la théorie des jeux (pour mieux analyser le monde)

La théorie des jeux est une preuve que les maths servent à quelque chose (pour ceux d’entre vous qui en voudraient un peu à cette noble matière) !

Dès le XIXème siècle, des mathématiciens ont créé des modèles pour simplifier des situations à priori compliquées. Ils ont cherché à expliquer des conflits politiques ou des relations humaines complexes en les assimilant à des sortes de jeux, plus simples, plus intuitifs. D’où le nom « théorie des jeux ».

Par exemple, la théorie des jeux peut-être utilisée pour simplifier la résolution d’un conflit diplomatique entre deux pays. Elle permet grossièrement de simplifier la variable humaine (notamment les réactions émotionnelles des protagonistes, qui sont difficiles à prévoir) et en réfléchissant de manière plus mathématique.

La diplomatie, c’est juste un exemple. Grâce à la théorie des jeux, on arrive ainsi à étudier non seulement des phénomènes politiques, mais également économiques et psychologiques !

[restrict paid=true]

Pourquoi les commerces du même type sont-ils toujours côte à côte ?

C’est vrai ça ! Pourquoi les magasins de souvenirs dans les villes touristiques sont-ils tous collés ? Pourquoi à côté d’un McDonalds il y a souvent un Quick ou un Burger King alors qu’il y a des quartiers entiers sans le moindre fast-food ?

Ce serait plus sympa pour nous s’ils étaient mieux répartis… Pour expliquer ce phénomène, jouons à un jeu !

Le jeu des vendeurs de glace

Pour vous offrir la voiture de vos rêves, vous décidez de passer votre été à vendre des glaces sur la plage. Il se trouve que votre voisin a eu la même idée et pose un stand strictement identique au vôtre sur le sable.

La solution la plus simple serait de vous partager la plage en deux : les vacanciers affamés se dirigeront vers le stand le plus proche et vous aurez à peu près le même profit à la fin du mois.

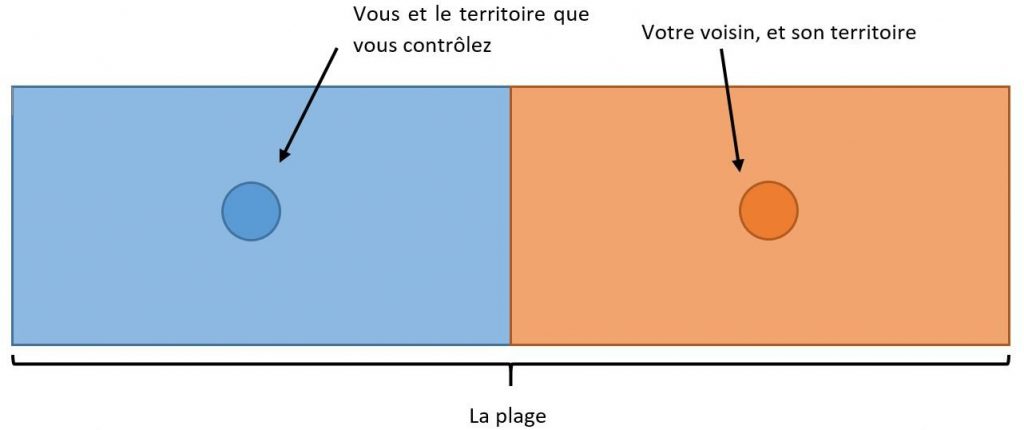
Mais malheureusement, votre voisin est en froid avec vous : il décide de déplacer son stand vers le centre de la plage pour récupérer certains de vos clients !

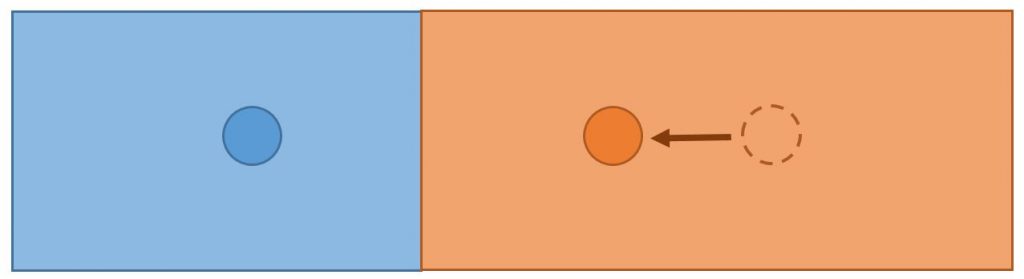
Comme vous ne vous laissez pas marcher sur les pieds, vous déplacez vous aussi votre stand vers le centre de la plage pour rétablir un équilibre.

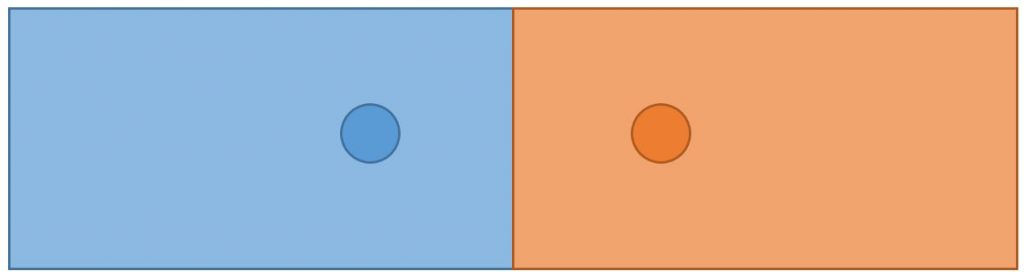
Si vous continuez à jouer à ce petit jeu, vous finirez par atteindre la situation d’équilibre où vous vous situez tous deux au centre de la plage.

Le moindre mouvement de l’un des deux « joueurs » lui serait alors défavorable. Un tel équilibre est appelé équilibre de Nash.

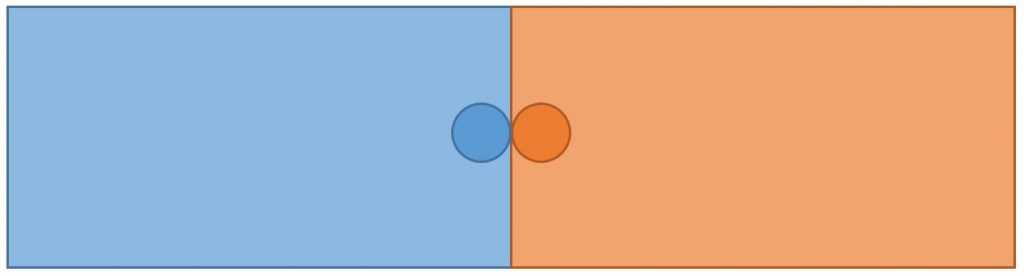
La théorie des jeux, c’est ça : modéliser un problème économique ou politique par un jeu, et trouver les différentes stratégies qui permettent de maximiser les gains (ici le nombre de clients que sert chaque stand).

À part vendre des glaces, ça sert à quoi en vrai ?

Ici, la théorie des jeux permet d’expliquer pourquoi des commerces du même type tendent à se regrouper au même endroit : on parle de principe de différentiation minimale.

Les magasins évitent alors de perdre des clients à cause d’une mauvaise localisation. Pour en gagner encore davantage, ils peuvent alors vendre des produits moins chers ou plus innovants : on parle de différentiation compétitive.

Le problème de la situation d’équilibre de ce jeu est qu’elle désavantage les clients aux extrémités de la plage : ils doivent parcourir la moitié de sa longueur pour avoir leur glace et risquent de se décourager.

La situation initiale était socialement plus optimale. Elle nécessite par contre que vous vous entendiez avec votre voisin.

Si vous décidez en plus de ne pas vous faire une guerre des prix, vous avez créé ce que l’on appelle un cartel. De telles pratiques sont en général interdites par les États car des ententes sur les prix nuisent au consommateur. Celui-ci doit payer plus que s’il y avait une concurrence libre.

Politique : la théorie des jeux pour obtenir plus de voix

Ce principe de différentiation minimale explique aussi pourquoi les partis politiques de droite proposent en période électorale des mesures de gauche et vice-versa.

En effet, si l’on considère que la population se répartit à peu près uniformément le long du spectre politique et que chacun vote pour le candidat avec les idées les plus proches des siennes, on revient au problème des marchands de glace.

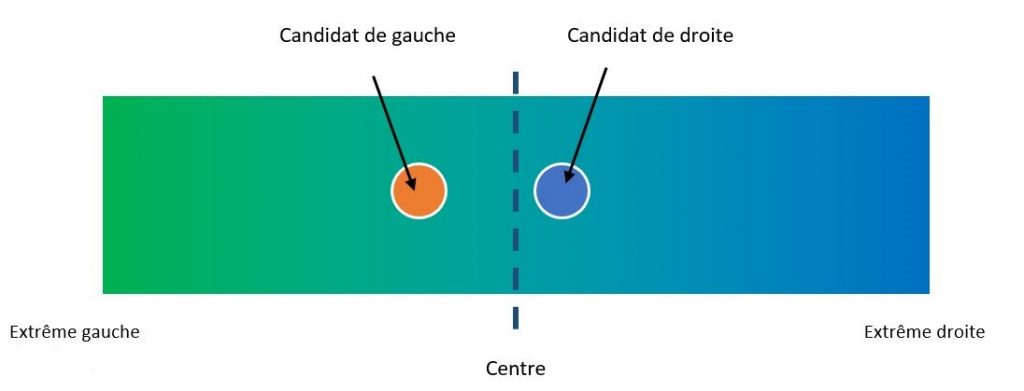
Dans cette situation, le candidat de gauche devrait proposer des idées plus libérales, sinon le candidat de droite risque de gagner…

Chaque candidat a alors intérêt à se rapprocher du centre du spectre politique pour attirer un maximum d’électeurs !

Géopolitique : comprendre la guerre froide avec la théorie des jeux

Dans la Guerre Froide, il y avait deux grands joueurs (pour simplifier) : les USA et l’URSS. Pendant près de 40 ans, ces deux superpuissances ont disposé de part et d’autre du rideau de fer des milliers de missiles nucléaires, et la construction de cet arsenal dissuasif a englouti des centaines de milliards de dollars.

Si les deux états avaient décidé dès le début des hostilités de ne pas se faire cette course à l’armement, beaucoup d’argent aurait pu être économisé ! Nous allons voir que tant que le climat était tendu entre les deux pays, l’escalade était quasiment inévitable.

Le dilemme du prisonnier : un paradoxe qui aide à mieux comprendre

Une fois de plus, nous allons modéliser la situation par un jeu, le dilemme du prisonnier. Sous sa version la plus courante, le jeu se présente sous la forme suivante :

Avec un complice, vous avez monté une escroquerie à grande échelle. Malheureusement, la police se doute de quelque chose et vous arrête tous les deux. Après vous avoir placé dans deux cellules différentes, ils vous proposent le dilemme suivant :

• Si vous avouez la fraude et votre complice avoue aussi, vous écoperez tous deux de cinq ans de prison
• Si vous avouez et que l’autre dément, vous serez libéré mais votre complice passera dix ans derrière les barreaux (et réciproquement)

Il reste aussi la possibilité qu’aucun de vous n’avoue, et manquant de preuves, la police vous relâche au bout de six mois.

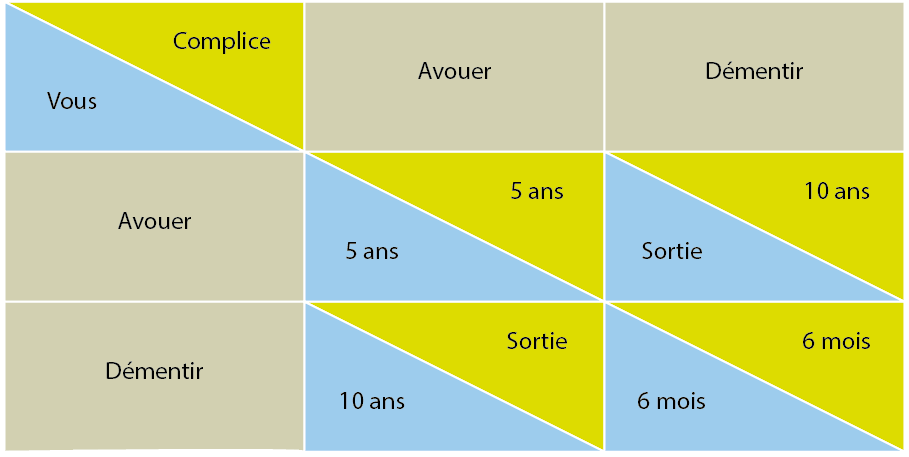
Le mieux pour vous deux serait de démentir tous les deux, mais malheureusement, ne pouvant vous parler, impossible de savoir si votre complice va coopérer…

Que faut-il faire si vous voulez sortir le plus rapidement possible ?

Pour répondre à cette question, étudions les différents cas :

• Si votre complice avoue, vous avez intérêt à avouer sinon vous passerez péniblement les dix prochaines années : vous passerez alors tous les deux 5 ans en prison.
• Si votre complice dément, vous avez aussi intérêt à avouer pour sortir tout de suite (et espérer que dans dix ans, votre associé ne se vengera pas trop violemment…)

Dans tous les cas, vous avez intérêt à avouer votre faute. Si les deux prisonniers font ce raisonnement, ils passeront tous deux cinq ans en prison et n’auront donc pas réussi à atteindre le compromis « optimal » où ils sont libérés au bout de six mois.

Le paradoxe est là : la solution toute indiquée par un raisonnement cartésien mène à une situation qui n’est pas la meilleure pour les deux joueurs.

Bien sûr, dans la réalité, la réputation de votre complice et l’idée que vous vous faites de lui vous permettra peut-être d’atteindre ce compromis si vous vous faites confiance. Par contre, si vous ne vous faites pas confiance, utiliser la théorie des jeux est utile pour passer le moins de temps possible sous les barreaux.

Quel est le rapport avec la guerre froide ?

La situation du début de la Guerre Froide ressemble un peu au dilemme du prisonnier. Les deux grandes puissances avaient le choix de déployer un arsenal militaire puissant ou non.

• Si tous deux déployaient des missiles, il y avait équilibre, mais beaucoup de pertes économiques (c’est la situation où les prisonniers ne se font pas confiance et avouent)
• Si tous deux n’en déployaient pas, il y avait aussi équilibre, et peu de gâchis de richesses (les prisonniers en se faisant confiance atteignent un optimum)
• Par contre, si seulement un pays installait un arsenal, il avait une nette supériorité et pouvait utiliser ce déséquilibre à son avantage (si l’un des prisonniers fait naïvement confiance à l’autre, il peut se faire avoir)

Tant que les deux pays ne se faisaient pas confiance, la solution indiquée par la théorie des jeux était de se protéger le plus possible. C’est ce qui s’est effectivement passé jusqu’à la détente et les accords SALT dans les années 70 où une confiance mutuelle a permis la désescalade.

Psychologie : marchander et influencer des choix

La théorie des jeux prédit le comportement de joueurs tout à fait rationnels. Comme nous ne sommes pas des machines, nous n’adoptons pas toujours la stratégie la plus raisonnable.

Lorsqu’il existe un écart entre ce qui est prévu par la théorie et la pratique, on peut penser qu’un phénomène psychologique a influencé notre décision. Prenons quelques exemples…

Le jeu de l’ultimatum : l’injustice ou l’argent

Le jeu de l’ultimatum se joue à deux : Alice dispose de 100 dollars, et doit faire deux tas avec : un tas pour elle de X dollars, un tas pour le second joueur Bob, de 100-X dollars. En gros, plus Alice prend d’argent, moins Bob en aura. Par exemple si Alice garde 70$ sur 100$, Bob ne pourra toucher que 30$.

Bob décide alors d’accepter ou non le partage :

• S’il accepte, Alice gagne ses x dollars et Bob 100-x.
• S’il refuse, aucun des deux joueurs ne gagne d’argent.

Ce jeu permet de représenter les situations économiques ou l’un des agents a un droit de véto, ou encore un boycott qui pénalise tout le monde.

En théorie, Bob a toujours intérêt à accepter le partage qui lui est proposé, car il gagnera toujours plus d’argent en acceptant qu’en refusant, ne serait-ce qu’un dollar !

Pourtant, lorsque le partage proposé est trop inéquitable, les joueurs ont tendance à le refuser. L’espèce humaine n’aime pas l’injustice, et nous refusons (parfois) les situations injustes même si nous gagnerions à les accepter. On parle d’aversion pour l’injustice.

L’aversion de la perte

Imaginons un autre jeu. Vous recevez 150 dollars, et on vous donne alors deux choix :

• Soit vous empochez les 150 dollars directement.
• Soit vous misez les 150 dollars dans un jeu de pile ou face, sachant que vous remportez 400 dollars si vous gagnez.

La théorie des jeux prédit mathématiquement qu’un joueur devrait miser son argent. En effet, en misant son argent, on gagne « en moyenne » 200 dollars, alors qu’en ne le misant pas, on gagne toujours 150 dollars.

Néanmoins, un bon nombre de joueurs décide de se contenter de 150 dollars, par peur de perdre cet argent : on parle d’aversion à la perte. On enseigne aux investisseurs de se méfier de cette peur qui les dissuaderait d’investir dans des placements pourtant prometteurs.

Dans ces deux exemples, la théorie des jeux permet de mettre en lumière des comportements humains en remarquant des écarts entre théorie et pratique dans des « jeux » simples.

En bref

La théorie des jeux permet en quelques sortes de schématiser des situations complexes. Elle permet de transformer une réalité pleine de nuances en un problème de logique mathématique plus simple à analyser.[/restrict]