La physique quantique est basée sur des phénomènes aléatoires et sur de nombreuses indéterminations. L’une d’elles est connue sous le nom de l’indétermination de Heisenberg.
Par « indétermination » on signifie ici que, quoi qu’on fasse, la mesure ne peut pas être plus précise que nous l’autorise la physique. L’indétermination de Heisenberg porte ainsi sur la vitesse (l’impulsion, en fait, qu’on approcherait classiquement par la vitesse) et la position d’une particule dans l’espace. Les deux ne sont pas mesurables ou connaissables de façon simultanée.
Pour faire simple, si on connaît la position d’une particule, alors sa vitesse sera indéterminée (et indéterminable). À l’inverse, on peut connaître la vitesse de la particule, mais alors ce sera sa position qui sera indéterminée.
Mathématiquement, tout cela revient à dire que l’incertitude sur la position (Δx) et l’incertitude sur la vitesse (sur l’impulsion, Δp) ne peuvent être infiniment petites à la fois :
Δx × Δp ≠ 0
En réalité, l’inégalité de Heisenberg est :
Δx × Δp ⩾ h/2π
Où h/2π étant une valeur constante.
On voit alors que si l’incertitude sur la position Δx diminue beaucoup, alors l’incertitude sur la vitesse Δp augmente de façon importante afin de satisfaire à l’inégalité. Même chose dans l’autre sens.
À l’origine de l’indétermination de Heisenberg: la dualité onde-particule
On peut se demander d’où tout ceci peut venir : après-tout, en mécanique classique, si on sait où se trouve notre voiture, on peut très bien en connaître la vitesse aussi…
Déjà, on l’a déjà dit mais c’est très important : le monde de la physique des particules ne réagit pas, ou n’est pas descriptible par les mêmes lois que la physique classique. La physique des particules est sujette à des comportements totalement contre-intuitifs.
Revenons à l’indétermination de Heisenberg : comment expliquer le fait qu’on ne puisse pas savoir simultanément où se trouve une particule et comment elle se déplace ? On peut expliquer ça avec la dualité onde-corpuscule de la lumière.
Au 17ème siècle, Newton pensait déjà que la lumière était une particule (comme des petites billes). Pratiquement à la même époque, Huygens pensait au contraire que la lumière était une onde. Sa renommée était telle que ce fut l’explication de Newton qui fut retenue durant plus d’un siècle.
Il a fallu attendre que Young et d’autres arrivent à faire interférer deux rayons de lumière et former des figures d’interférences, comme on peut faire interférer des vagues (des ondes également) à la surface de l’eau, pour contrer la théorie de Newton. Il n’était alors plus question de lumière sous forme de particules, mais uniquement sous la forme d’ondes.

On illustre souvent la notion de figures d’interférence avec les ondes que forment des mouvements dans l’eau à la surface d’un étang.
C’est finalement grâce à Einstein, au début du XXe siècle, que la théorie corpusculaire de la lumière fut de nouveau remise sur la table : Einstein avait montré que la lumière pouvait interagir avec la matière, par exemple lors de l’effet photoélectrique (les panneaux solaires). Ces phénomènes montrent que la lumière heurte les électrons comme des particules normales.
Alors que faire ?
D’un côté, les expériences de Young étaient la preuve que la lumière était une onde et de l’autre côté, les travaux d’Einstein montraient que la lumière était faite de particules : les photons.
C’est De Broglie en 1924 qui arrivera à concilier les deux idées : il montra durant sa thèse que la lumière était quelque chose qui pouvait être soit une onde, soit une particule, selon l’expérience ; et qu’en réalité le photon était quelque chose d’autre qu’il nommera « paquet d’onde ». Plus tard, il montrera que la même chose est vraie pour les électrons, les atomes et même des molécules entières !
Mais comment c’est possible ? Et en quoi ça m’aide à comprendre l’indétermination de Heisenberg ?
Vous vous souvenez de l’indétermination ? Elle dit qu’une particule ne peut à la fois livrer sa position et sa vitesse. Autrement dit, même avec toute la bonne volonté du monde, il vous serait impossible de calculer à la fois la vitesse et la position d’une particule.
Selon De Broglie, une particule peut être soit une onde :
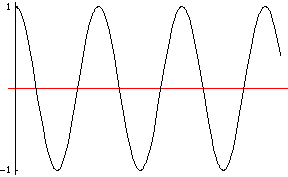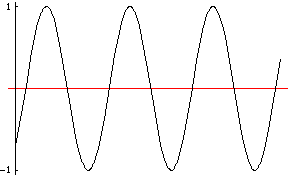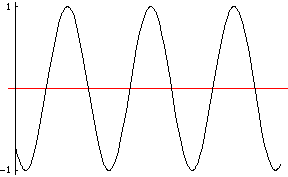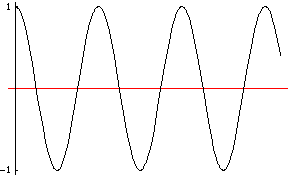
Onde progressive (qui se propage)
Soit un paquet d’onde (un paquet d’onde représente une particule de manière ondulatoire) :

Un paquet d’onde (qui se déplace)
Posez-vous deux questions :
- Sur l’onde (image n°1), quelle est sa vitesse de propagation ? C’est simple : il suffit de voir combien de temps il s’écoule entre deux crêtes, de mesurer la longueur de l’onde, de faire une petite division et on a la vitesse de propagation de l’onde.
- Sur le paquet d’onde (image n°2), quelle est sa position ? Facile : le paquet d’onde est à l’endroit où il apparaît sur la courbe, c’est à dire là où le trait n’est pas « plat ».
Et maintenant :
- L’onde (image n°1), où est-elle ? On ne sait pas : elle est partout.
- Le paquet d’onde (image n°2), quelle est sa vitesse de propagation ? On ne sait pas, on ne peut même pas parler de propagation : impossible de mesurer la durée entre deux crêtes, ces dernières ne sont jamais les mêmes en un point donné et finissent même par disparaître !
C’est donc simple : l’onde possède une vitesse parfaitement définie mais elle est partout, et le paquet d’onde a une localisation très précise mais a une vitesse vaguement définie (sans mauvais jeu de mot).
Dans la réalité, c’est ce qui se passe c’est qu’on observe des paquets d’ondes. En observant un seul paquet d’onde, on observe comme une particule d’énergie (photon) et en observant un flux continu d’énergie (plusieurs paquets d’ondes à la suite, donc collés, donc formant comme une onde « entière ») on observe une onde.
Pour résumer
L’indétermination de Heisenberg est liée au phénomène de dualité onde-particule de la lumière et le fait qu’il n’est en fait ni l’un ni l’autre mais plutôt un « paquet d’onde ».
Que ce soit la lumière, l’électron ou même un atome entier, soit il est localisé sans avoir de vitesse précise, soit on ne sait pas trop où il est mais on peut mesurer sa vitesse (avec sa longueur d’onde) avec une grande précision.

11 Commentaires
nico
3 mars 2015 à 16 h 04 minL’explication avec l’onde progressive et le paquet d’onde me laisse perplexe.
Le paquet d’onde a une vitesse facile à déterminer, d’autant plus que sa vitesse de phase et sa vitesse de groupe sont les mêmes.
Si on continue à compresser le paquet d’onde, on voit aussi un pic se déplacer, et la vitesse de ce pic est facilement calculable.
Ce n’est donc pas la vitesse visible des pics qui importe.
Je pense que l’explication originelle n’a pas été comprise et a été réécrite de manière incorrecte.
L’explication est plutôt la suivante:
En mécanique quantique, mesurer une quantité (la vitesse ou la position) se fait en appliquant un opérateur. Le résultat est une fonction.
On peut avoir un système 1 tel que si on applique l’opérateur position sur ce système, on obtient la fonction correspondant à la première image. Cette première image correspond à la densité de probabilité de la position: la particule a plus de chance de se trouver aux pics de la sinusoïde. On a donc autant de probabilité d’avoir la particule sur le pic de droite que sur le pic de gauche, l’incertitude sur la position est grande.
On peut avoir un système 2 tel que si on applique l’opérateur position sur ce système, on obtient la fonction correspondant à la deuxième image. Dans ce cas, l’incertitude sur la position est plus petite (car on sait qu’on a plus de chance d’être au milieu du paquet que sur les bords, et une chance nulle d’être ailleurs).
On peut aussi avoir un troisième système 3 où la fonction correspondante est une fonction delta de Dirac: un pic parfaitement localisé. On a alors une précision très importante sur la position.
Le principe d’incertitude dit simplement que pour le système 1 (où l’incertitude sur la position est très grande), lorsqu’on applique l’opérateur quantité de mouvement (équivalant à la vitesse), on obtient une fonction delta de Dirac, c-à-d une précision très importante sur la vitesse.
Et inversément, pour le système 3, on obtient avec l’opérateur quantité de mouvement une sinusoïde.
Pour le système 2, le paquet d’onde a une incertitude similaire sur la position et sur la vitesse.
En fait, montrer ces ondes ne sert à rien tant qu’on ne donne pas la relation entre les 2 opérateurs « position » et « quantité de mouvement ».
Pour ces dessins, la relation correspond à la fréquence (transformée de Fourier):
Dans le premier dessin, on a 1 onde avec 1 fréquence bien définie -> 1 valeur pour la vitesse -> peu d’incertitude.
Dans le second dessin, on a 1 onde qui correspond à la somme de plusieurs ondes de fréquence différente -> chacune de ces fréquence est possible avec une certaine probabilité -> beaucoup d’incertitude.
Mais la vitesse visible du pic de l’onde ne change rien: une particule avec une grande vitesse ou une petite vitesse peut être représentée par la même vitesse visible du pic (mais les pics sont plus ou moins nombreux).
(corrigez moi si je me trompe)
Timo van Neerden
3 mars 2015 à 19 h 29 min« Dans le premier dessin, on a 1 onde avec 1 fréquence bien définie -> 1 valeur pour la vitesse -> peu d’incertitude.
Dans le second dessin, on a 1 onde qui correspond à la somme de plusieurs ondes de fréquence différente -> chacune de ces fréquence est possible avec une certaine probabilité -> beaucoup d’incertitude. »
La fréquence d’une onde c’est l’énergie qu’elle véhicule, et son énergie peut être liée à son impulsion quand on revient au modèle du paquet d’onde.
Avoir une incertitude sur la fréquence dans le paquet d’ondes, revient à avoir une incertitude sur son impulsion.
La quantité de mouvement d’un photon n’est pas nulle en fait, même si sa masse l’est (un photon peut communiquer une partie de son impulsion à un électron par exemple, c’est l’effet Compton). On résout ce problème en nommant cette grandeur « impulsion » et en lui donnant une définition plus cohérente par rapport aux propriétés des photons (sans faire intervenir la masse, mais plutôt le vecteur d’onde, la constante de Planck… ).
Dans l’article je confond (consciemment) la vitesse d’un photon avec la notion d’impulsion : tout simplement parce l’impulsion est l’équivalent ondulatoire de la quantité de mouvement (et donc « un peu » de la vitesse) en mécanique newtonienne. C’est juste pour simplifier tout ça. Je ne sais pas trop encore qui lit mes articles, mais dans le sens où je veux vulgariser quand même un peu, je me refuse de trop m’enfoncer dans les détails et les calculs (je suis d’ailleurs incapable de faire la plus grande partie des maths en physique quantique…).
nico
3 mars 2015 à 22 h 18 min« Avoir une incertitude sur la fréquence dans le paquet d’ondes, revient à avoir une incertitude sur son impulsion. »
Je suis totalement d’accord avec ça, c’est justement ce que je dis: peu importe la vitesse de propagation visible sur les gifs animés, ce qui compte, c’est la fréquence de l’onde.
Or, le texte parle de vitesse de propagation (ce qui est renforcé par l’animation).
Dans le second dessin, il est facile de calculer une vitesse de propagation: soit la vitesse de groupe, soit la vitesse de phase, qui sont d’ailleurs identiques ici.
C’est incorrect de dire que la vitesse de propagation du second dessin est incertaine, elle est facile à calculer.
Par contre, c’est vrai que la fréquence est incertaine. Et c’est justement la fréquence qui est liée à la quantité de mouvement. C’est ça qui me chiffonne dans ces explications: le mouvement de l’onde sur les gifs animés est confondue avec la vitesse de la particule.
(ou, en d’autres termes: le dessin 1 pourrait représenter une onde stationnaire, cela ne voudrait pas dire que la particule a une vitesse nulle)
Pas de problème à vulgariser. Mais ici, lorsqu’on lit le texte, on lit que le mouvement sur les gifs animés correspond au mouvement (et donc la vitesse) de la particule, alors que ce qui correspond au mouvement (et donc la vitesse) est la fréquence de l’onde.
Je pense qu’il y a aussi une erreur d’interprétation de ces dessins: ceux-ci représentent la fonction d’onde, c-à-d la densité de probabilité pour les valeurs sur l’axe x qui correspond à l’observable étudiée (et encore, cette fonction d’onde est complexe alors que seule la partie réelle est illustrée), pas d’une onde de matière ou électromagnétique, ce qui est différent.
nico
12 mars 2015 à 1 h 16 minok, p-e que j’ai noyé ma question dans mes commentaires précédents.
Sur la deuxième image, je vois une onde qui bouge, où la vitesse de propagation est parfaitement définie (soit via la formule de vitesse de phase, soit via la formule de vitesse de groupe, qui sont, dans ce cas, identiques).
Or, le texte dit que la vitesse de propagation n’est pas déterminée dans le deuxième cas.
Quelle est l’explication dans ce cas ?
Le bg
14 décembre 2015 à 18 h 25 minPeut on m’expliquer pourquoi l’on ne peut pas tout simplement faire deux mesures distinctes sur un même objet qui nous donneraient chacune une des deux informations afin de connaître vitesse et position?
Timo van Neerden
14 décembre 2015 à 19 h 20 minAbsolument : parce que la première mesure va fausser la seconde mesure, tout simplement.
Si on mesure la position d’une particule, l’appareil de mesure (quel qu’il soit) va modifier sa trajectoire ou d’autres propriétés de cette particule.
Et ça marche pour tout : si tu as une bassine d’eau, que tu veuilles en connaître la température, tu vas y plonger ton thermomètre.
Sauf que… le thermomètre, en prenant la température de l’eau va modifier la température de cette eau : si l’eau est en réalité à 50 °C et le thermomètre à 20 °C, alors si on plonge le thermomètre dans l’eau, les deux vont s’équilibrer à environ 49,99999999 °C : la mesure est faussée.
Une façon de contourner le problème serait de chauffer le thermomètre à 50 °C avant de la plonger dans l’eau. Mais, hé ! Comment on sait qu’il faut la chauffer à 50 °C et non à 55 °C ? On ne sait pas, car c’est justement pour ça qu’on veut plonger le thermomètre dans l’eau !
Et il n’est pas possible d’éviter cette erreur de mesure : si on utilise un thermomètre infra-rouge, alors on mesure la chaleur qui s’échappe de l’eau. Or, si de la chaleur s’échappe de l’eau, l’eau refroidit, et donc la mesure n’est plus à jour. Il y aura toujours une erreur, quelque soit la méthode. La science de la mesure (métrologie) consiste à deux choses : 1) à défaut de pouvoir la supprimer, il faut réduire le plus possible cette erreur et 2) savoir quantifier cette erreur.
La véritable solution est donc d’utiliser un thermomètre le plus sensible possible (pour quantifier le plus précisément possible la température), le plus précis possible (pour quantifier l’erreur la plus précisément possible) et qui modifie le moins possible la température de l’eau (pour réduire cette erreur — un thermomètre le plus petit possible est une solution pour ça). Et évidemment, un tel thermomètre coûte cher.
Quand il s’agit de mesurer des positions ou des vitesses de particules, l’erreur commise est énorme. Dans le cas d’un photon par exemple, on ne sait qu’il est présent que si on l’absorbe. La simple mesure de sa présence suffit à le faire disparaître. Dans ce cas là, impossible de faire deux mesures.
[email protected]
16 décembre 2015 à 11 h 58 minBonjour, je n’y connais absolument RIEN en physique quantique mais votre blog est passionnant. Je comprends que cela remettrait en cause beaucoup de point de la physique classique mais je voulais savoir ce que l’indétermination d’Heisenberg nous apportait, ou nous permettait de comprendre? ça nous permettrait de remettre toujours en cause certains résultat? De dire qu’on jamais sûre à 100% de tout ce qu’on connaît?
Timo van Neerden
16 décembre 2015 à 18 h 37 minL’indétermination de Heisenberg met un arrêt à l’espoir qu’avaient les anciens physiciens (avant le XXe siècle, en particulier Laplace) sur un modèle parfaitement déterministe de l’univers.
En physique classique, si je laisse tomber une pomme, elle tombe. Si j’en laisse tomber une autre, elle tombe aussi. Elle tomberont toutes, et toujours selon la même vitesse. Ceci nous permet, avant de faire l’expérience, de prédire ce qui va se passer : « que se passe-t-il si je lâche un pomme ? » réponse : « elle va tomber de telle façon avec telle vitesse ».
En gros, en connaissant un état initial (pomme en l’air) on pouvait déterminer ce qui en découlait (pomme qui tombe). On a donc une relation de cause à effet parfaitement claire.
Les physiciens avant le XXe siècle se demandaient si l’univers tout entier réagissait de la sorte. Laplace se demandait même si connaître toutes les caractéristiques (vitesse, position…) de toutes les particules de l’univers permettait d’en déduire le futur de l’univers, y compris les comportements humains. Connaître tout ça permettait donc de savoir absolument tout ce qui va se passer dans l’univers.
Bien-sûr, connaître l’ensemble des caractéristiques de l’ensemble des particules de l’univers, c’est compliqué (pour ne pas dire impossible).
L’indétermination de Heisenberg dit désormais qu’un tel raisonnement est impossible, car on ne peut même pas connaître toutes les caractéristiques d’une seule particule, donc de toutes les particules… c’est encore moins possible.
Certains y voyaient et y voient une preuve que Dieu existe : Même si Dieu aurait créé l’univers avec des lois et des règles que toutes les particules obéissent, cette indétermination de Heisenberg lui laissaient une façon d’agir sur l’univers et de changer certaines choses, malgré les règles qu’il a lui-même énoncé lors de la création.
Ce qui en découle de l’impossibilité de connaître parfaitement une particule, c’est donc que l’univers et son évolution conservent une part d’aléatoire et d’inconnu : qu’il y aura toujours quelque chose qui ne sera pas possible de déterminer, à cause des phénomènes quantiques qui ont lieu au cœur de la matière.
On peut donner les grandes lignes de l’évolution d’une pomme, d’un train, d’une planète ou d’une galaxie, et ce qu’on peut savoir suffit très largement pour nos applications, mais fondamentalement, il n’est pas possible de savoir où sera telle ou telle particule dans 100 ans, par exemple.
Mais, je me répète, l’indétermination de Heisenberg a lieue au niveau des particules : elle n’empêche pas de connaître la trajectoire d’une pomme ou de tout autre objet de taille « normale ».
On ne peut pas connaître à 100% une particule. Mais ça s’arrête là.
Tout est fait de particules, donc même une pomme ne sera pas descriptible à 100% au niveau atomique, mais ça reste une pomme au sens d’objet macroscopique.
L’indétermination de Heisenberg — ainsi que tous les effets quantiques « bizarres » — n’ont de véritable sens QUE dans le monde de la physique des particules.
nico
20 décembre 2015 à 14 h 29 minC’est une réponse un peu caricaturale.
Tout d’abord, la situation actuelle est très proche d’une situation « sans principe d’indétermination ». Aujourd’hui, on sait que mesurer une grandeur sans erreur est impossible, et on sait qu’une petite variation dans un système complexe peut entraîner un grand écart sur la prédiction (sans parler du problème philosophique d’induction de Hume).
Donc, les physiciens s’en foutent un peu des conséquences pratiques de l’indétermination d’Heisenberg. Il est par exemple faux de penser que les physiciens ont été déçus de savoir qu’ils ne pourront pas prédire absolument un résultat, car ils savaient très bien que c’était déjà le cas avant l’essor de la mécanique quantique.
Et rappelons qu’en pratique, les mesures les plus précises effectuées par l’homme sont des mesures de propriété quantique. Non, la précision n’est pas remise en cause par la mécanique quantique.
Mais surtout, le déterminisme n’est PAS remis en cause par la physique quantique (c’est d’ailleurs également expliqué sur wikipedia: https://fr.wikipedia.org/wiki/Déterminisme#Physique_quantique )
Les fonctions d’onde de probabilité de la théorie quantique des champs sont totalement déterministes. Et comme la vitesse et la position sont simplement, en mécanique quantique, pas des propriétés fondamentales, cela ne pose pas de problèmes.
(note en passant: certaines personnes ont été rassurés par le principe d’indétermination, car selon eux, cela leur permet de nouveau de croire dans le libre arbitre. Mais ça ne marche pas non plus: le libre arbitre, c’est quand l’individu est capable d’influencer lui-même ses propres choix. Dans un déterminisme classique, le choix est: vu votre état physique actuel, vous avez 100% de chance de faire le choix A. Dans un déterminisme quantique, le choix est: vu votre état physique actuel, vous avez 64% de chance de faire le choix A et 36% de faire le choix B. Dans les deux cas, l’individu ne choisit pas son propre choix)
Roger
6 octobre 2017 à 16 h 25 minNico j’arrive pas à comprendre ton argumentation. C’est probablement parce que je ne comprend pas quelques termes ou idées, car je suis un éleve espagnol. Je suis en train de faire un travail sur la physique quantique et ta vision m’interesse. Est-ce que tu peut me contacter?
[email protected]
Et est-ce que se video te semble correcte? Est-ce qu’il explique bien ce principe et est-ce qu’il est d’accord avec tes idées?
https://www.youtube.com/watch?v=TQKELOE9eY4
planetpixel
9 juillet 2018 à 12 h 06 minBonjour Timo,
J’suis d’accord, J’suis d’accord, J’suis d’accord!
Néanmoins, il est tout à fait possible de déterminer la vitesse de déplacement d’un paquet,
il suffit de mesurer le temps écoulé entre 2 points.
Toi qui fait de l’info ne peut l’ignorer …
: )